Box-Cox変換とRankGaussc法:データを正規分布に近づけたい
例えば、購買データなどを扱っているときには対数正規分布に似た裾の重い分布(heavy-tail-distribution)がよく表れます。
裾が重いということは平均から大きく外れた値が無視できない確率で発生するということです。
身近な例でいえば各世帯の貯蓄額の分布などがそうなります。次のグラフのように、多くの人はグラフの左側に分布していてそれほど大きな貯蓄はないが、上を見るといくらでも貯蓄額の大きな人がいて青天井という状況です(貯蓄や所得のこのような状況はパレート分布でモデリングされます)。
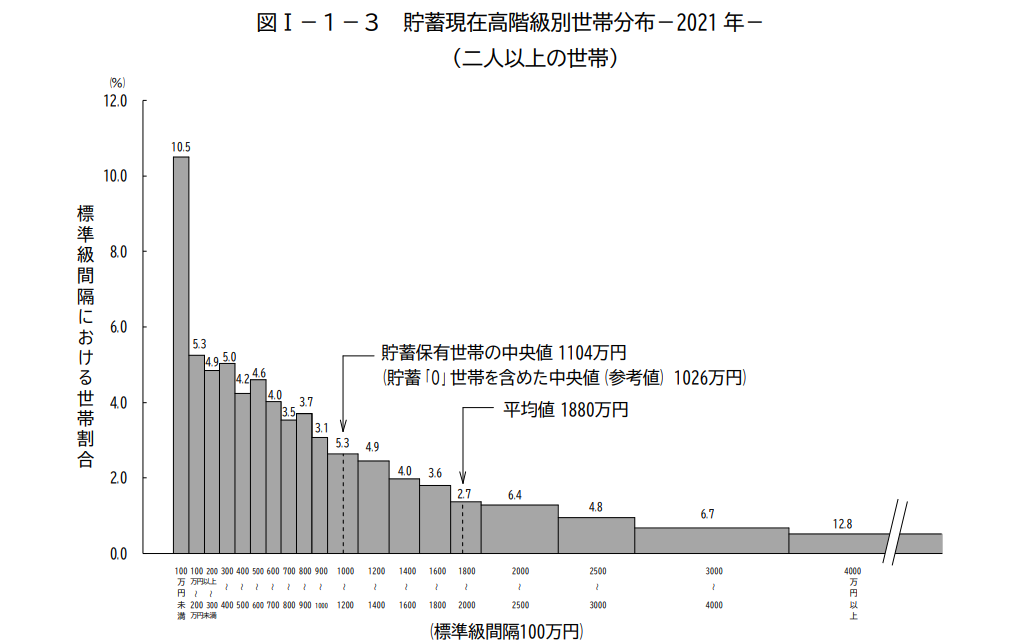
このようなデータは、平均から大きく外れているものの外れ値とは言えないデータの影響で標本平均がぶれやすい性質があります。
そこで、一度何らかの変換を施してデータを正規分布に近づけて処理します。
そんなときに使用できる手法の2つを試したので備忘録ついでにまとめておきます。
Box-Cox変換とRankGauss法:データの準備
下図は適当に生成したデータをヒストグラムにしたものです。
Rライブラリのmiceaddsに含まれているfleishman_sim関数を用いると、平均や分散だけでなく歪度や尖度まで指定してnon-normalな乱数を生成することができます。
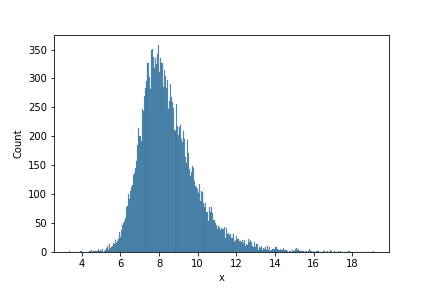
以下、Rで乱数を生成する際のコード。
# install.packages('miceadds')
library(miceadds)
sample_size <- 20000
rand <- fleishman_sim(sample_size, mean=8.5, sd=1.5, skew=1.2, kurt=3.1)
(※本記事では乱数の生成以外はPyhtonで分析しています。non-normalな乱数の生成にmiceaddsを使いたかっただけなのでRはここでしか出てきません)
sample_sales_dist.csv:csvデータを置いておくので必要に応じて使用してください。
さて、このデータだけではheavy-tail-distributionにはなっていません。実際に現れる購買データに近いデータにするためにはこれを指数関数に代入します。
import numpy as np
import pandas as pd
import seaborn as sns
df = pd.read_csv('/hoge/sample_sales_dist.csv') # ファイルを適当なディレクトリにおいて読み込む
df['x_powered'] = 2 ** df[['x']]
sns.histplot(df.x_powered, binwidth=1500)
ここでは指数関数の底を2にしていますが深い理由はなく、生成されるデータがそれっぽくなるように選んだだけです。出力されるグラフは下になります。
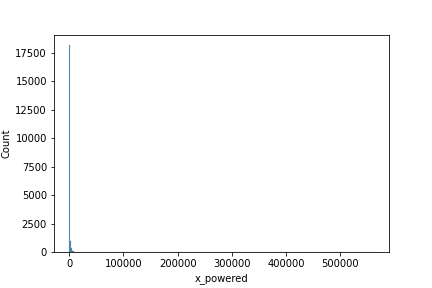
ほとんどの要素がグラフの左側に配置されてつぶれたヒストグラムになっています。あまり綺麗ではないですが、実際に分析しているとよく見かける形です。
10,000以上の大きな値が無視できない確率で発生するのでどうしても右側の裾が長くなる(=裾が重い)ヒストグラムになります。
clipingして一定以上の値をすべて同じ階級に丸め込んでしまえばもう少し見やすいヒストグラムになります。
sns.histplot(df.x_powered.clip(None, 10000), binwidth=100)
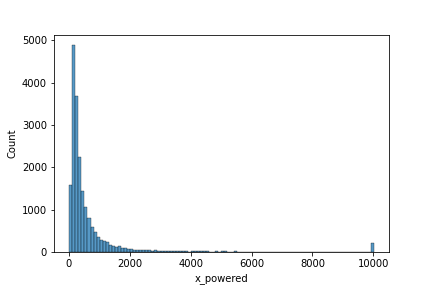
このデータを何とかして正規分布に近づけようとするのがBox-Cox変換とRankGauss法です。
今回はデータの作成に指数関数を用いたので対数をとればそれなりに綺麗なデータになる(図1)ことはわかっていますが、それでも尖度や歪度が0でないので正規分布になっているわけではありません。
それでは、Box-Cox変換とRankGauss法を用いるとどうなるのか試してみます。これらの手法は次の書籍で紹介されています。
Box-Cox変換
Box-Cox変換は下記で定義されます。
\begin{align}
t_{\lambda} (x) = \left\{
\begin{array}{ll}
\frac{x^{\lambda} – 1}{\lambda} & (\lambda \neq 0)\\
\log x & (\lambda = 0).
\end{array}
\right.
\end{align}
ハイパーパラメータ\(\lambda\)がありますが、scipyの関数boxcoxを使えば自動で計算してくれます。
from scipy.stats import boxcox # Box-Cox変換を実行 df['x_boxcox'], best_param = boxcox(df.x_powered) # 描画 sns.distplot(df.x_boxcox, kde=False, rug=False)
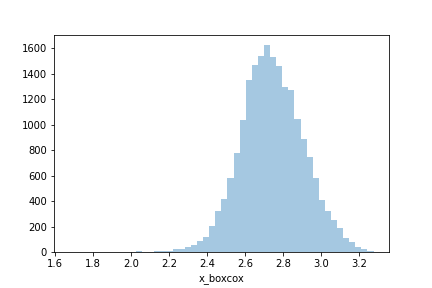
変換を施すことによってかなり綺麗なヒストグラムになりました。
ただし、歪度と尖度を見てみると歪度は0に近くなっているものの尖度に関しては0に近いとは言えなさそうです。
print(f'skewness : {df.x_boxcox.skew()}')
print(f'kurtsis : {df.x_boxcox.kurt()}')
# > skewness : -0.013651861601343388
# > kurtsis : 0.36535633706540205
ただ歪度が0に近いということは左右対称に近い分布になっているのでこれだけでもかなり扱いやすくはなっています。Box-Cox変換の良いところは変換がシンプルなことでしょうか。
では、もっと正規分布に近い分布に変換することはできるかというと、できます。RankGaussを実行してみましょう。
RankGauss法
from sklearn.preprocessing import QuantileTransformer transformer = QuantileTransformer(random_state=0, output_distribution='normal') transformer.fit(df[['x_powered']]) df['x_rankgauss'] = transformer.transform(df[['x_powered']]) sns.distplot(df.x_rankgauss, kde=False, rug=False)
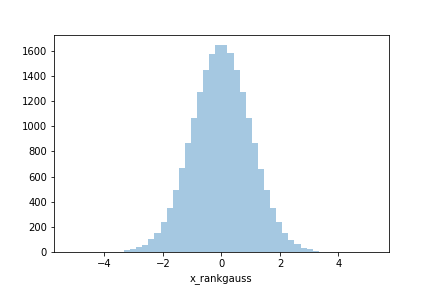
かなり正規分布に近いヒストグラムになっているように見えます。
歪度も尖度もBox-Cox変化に比較して0に近くなっています。
print(f'skewness : {df.x_rankgauss.skew()}')
print(f'kurtsis : {df.x_rankgauss.kurt()}')
# > skewness : -0.0036438824647088627
# > kurtsis : 0.004099295833516425
RankGaussではもとのデータにランクを付与し、そのランクから正規分布になるように無理矢理変換を加えるのでBox-Coxほどシンプルではありません。
データ間の間隔情報はBox-Coxより失われているので、使うときには失われた情報が本質的でないか検討しながら使う必要がありそうです。
参考文献
[1] 門脇大輔, 阪田隆司, 保坂佳佑, 平松雄司, Kaggleで勝つデータ分析の技術, 技術評論社.
[2] 総務省, https://www.stat.go.jp/data/sav/sokuhou/nen/pdf/2021_gai2.pdf