線形回帰で効果検証
現在仕事で効果検証を担当しています. 効果検証において重要なことは「いかに選択バイアスをなくすか」です. 最良なのはランダム化比較実験(RCT)ですが, 環境が整わずRCTが実行できないことも少なくありません.
そんなときに検討すべき手法の1つが回帰分析です. 効果検証や因果推論の書籍を見て回帰分析が出てこないことはまずありません(おすすめの書籍はこちらの記事をどうぞ).
そんな回帰分析の基本が線形回帰であるということで, この記事では線形回帰に親しんでみようと思います.
線形回帰で効果検証:効果があるとは?
まずは基本を押さえたいと思います. 次のようなモデルを考えたいと思います.
$$
Y = 3 X + 3Z + \rm{err},
$$
主要部は\(Y = 3 X\)であり, これは\(X\)が大きくなるほど\(Y\)も大きくなるといっています. たとえば, 小学生の学年と身長, 顧客数と売上などです. \(Y\)を目的変数といい\(X\)を共変量と言います.
\(X\)は機械学習で説明変数と呼ばれるものと同じですが, 効果検証では\(Y\)を説明するというよりは\(X\)による余分な影響を無視するために導入されるので共変量(=共に変化する余分な量というニュアンスだと思います)と呼ばれることが多いです.
それに対し\(Z\)は介入変数と呼ばれます. \(Z = 0,1\)の二値しかとらず, これは介入があったかどうか, つまり施策を実行したかどうかだけを表します.
実はここがキモで, 効果検証で回帰分析を行う時には必ずこの介入変数が含まれます(「介入なくして因果なし」ですから当然ですが). つまり, 効果検証で回帰分析というと最低でも共変量 + 介入変数の2つがありますから, 必ず重回帰になります.
さて, \(Z\)の値でどう変化するのか見てみましょう. たとえるなら何らかのキャンペーンを行って顧客の売り上げが全体的に伸長したと考えられます.
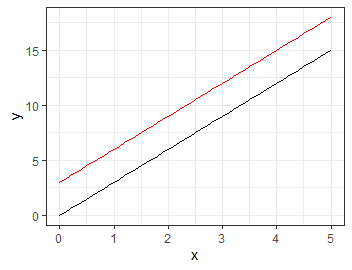
介入変数が1のときに全体の売上が3ずつ増加している様子です.
最後に\(\rm{err}\)は誤差を表しており, これらの直線をもとに多少\(Y\)がぶれる様子を表します.
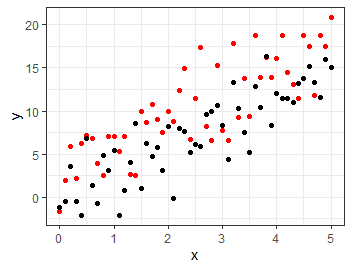
実際にデータを生成してみるとこのようになります.
このように, 介入変数の係数が0でない値をとるときにその介入は効果があったといえます. もっと言うと, 効果検証における回帰分析では介入変数の係数にしか興味がありません. 共変量に指定している時点で共変量が目的変数に影響を与えることはわかっているので, 影響が未知なのは介入変数だけだからです.
線形回帰で効果検証:実際に検証してみる
それではRコードを交えて実際に効果検証してみます.
ひとまず先ほど作成したデータを作るためのコードを確認してみます.
# ライブラリ library(tidyverse) library(broom)
# データの作成 #### x <- seq(0,5,0.1) #[0,5]区間を0.1ずつ分割. err_treat <- rnorm(x %>% length(), sd=3) # 乱数を発生させる. err_ctrl <- rnorm(x %>% length(), sd=3) y_treat <- 3 * x + 3 + err_treat y_ctrl <- 3 * x + 0 + err_ctrl # 作図して分布を確認 df <- data.frame( x = x, y_treat = y_treat, y_ctrl = y_ctrl ) ggplot(df) + geom_point(aes(x=x, y=y_treat), color='red') + geom_point(aes(x=x, y=y_ctrl)) + theme_bw() + labs(y='y')
では, 線形回帰を実行して結果を見てみます. ここではbroomパッケージのtidy関数を使用して線形回帰の結果を見やすく取り出しています.
# 線形回帰 #### x <- c(x, x) y <- c(y_treat, y_ctrl) z <- c( rep(1, x_treat %>% length()), rep(0, x_ctrl %>% length()) ) res_lm <- lm(y ~ x + z) res_lm %>% summary() %>% tidy()
# 結果 # A tibble: 3 x 5 # term estimate std.error statistic p.value # <chr> <dbl> <dbl> <dbl> <dbl> #1 (Intercept) 0.218 0.748 0.291 7.71e- 1 #2 x 3.20 0.230 13.9 4.56e-25 #3 z 2.69 0.677 3.98 1.31e- 4
先ほど述べたように効果検証における回帰分析では介入変数の係数にしか興味がありません.
つまり, 一番下の行のzだけをみます. 推定量は2.69でありp値は1.31e- 4となっています. 言い換えれば, この介入によって\(Y\)は有意に変化し, その変化量はおよそ2.69の増加だと言っています.
いま私たちは真の増加量が3であることを知っているので, 推定量として大きく外れていないことがわかります.
ただ, std.error, つまり標準誤差を見てみると0.677となっています. 標準誤差は推定量の標準偏差ですから, おおざっぱな計算ですが1.3 ~ 4.1くらいの間であれば真の値(=ここでは3)が高い確率で入っていそうだと言っています. ちょっと標準誤差が大きいですね.
線形回帰で効果検証:誤差が大きくなると標準誤差はどうなる?
上の例では\(\rm{err}\)の標準偏差を3にしてありました.
再掲しますが下図を見てもわかる通り, 真のグラフから離れている(=ばらつきが大きい)データがわりとあります.

なんとなく\(\rm{err}\)の標準偏差が小さいほうが標準誤差も少なくなりそうだという気がします. それを確かめてみましょう.
# errの標準偏差を指定すると, 上でやった分析と同じ分析を行ってその標準誤差を返す関数
effect_predict <- function(sd) {
x <- seq(0, 5, 0.1)
err_treat <- rnorm(x %>% length(), sd=sd)
err_ctrl <- rnorm(x %>% length(), sd=sd)
y_treat <- 3 * x + 3 + err_treat
y_ctrl <- 3 * x + 0 + err_ctrl
x <- c(x, x)
y <- c(y_treat, y_ctrl)
z <- c(
rep(1, x_treat %>% length()),
rep(0, x_ctrl %>% length())
)
res_lm <- lm(y ~ x + z)
res_lm %>%
summary() %>%
tidy() %>%
pull(std.error) %>%
tail(1) %>% # 最後の要素を取得
return()
}
これを\(\rm{err}\)の標準偏差を変えながら何度も実行してみます.
res_err <- c()
sd_params <- 1:30
for (sd in sd_params) {
res_err <- effect_predict(sd) %>% append(res_err, .)
}
df <- data.frame(
sd = sd_params,
std_error = res_err
)
ggplot(df, aes(x=sd, y=std_error)) +
geom_line() +
theme_bw()
この結果は以下になります.
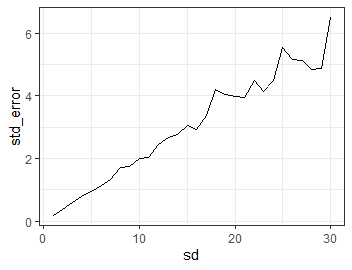
やはり\(\rm{err}\)の標準偏差が大きくなるほど標準誤差も大きくなるようです.
とても直感的に納得のいく結果になりました.
線形回帰で効果検証:おまけ
線形回帰を応用すると真の関数がもっと変な形をしていても回帰分析を行うことができます.
\(\rm{sin(x)}\)を中心に発生したデータで線形回帰してみます. やり方としては線形回帰に使用する\(x\)を\(\rm{sin}(x)\)に取り換えるだけです.
x <- seq(0,7,0.1) err_treat <- rnorm(x %>% length(), sd=1) err_ctrl <- rnorm(x %>% length(), sd=1) y_treat <- 2*sin(x) + 3 + err_treat y_ctrl <- 2*sin(x) + 0 + err_ctrl df <- data.frame( x=x, y_treat=y_treat, y_ctrl=y_ctrl, treat_gen=2*sin(x) + 3, ctrl_gen=2*sin(x) ) ggplot(df) + geom_point(aes(x=x, y=y_treat)) + geom_point(aes(x=x, y=y_ctrl), color='red') + geom_line(aes(x=x, y=treat_gen)) + geom_line(aes(x=x, y=ctrl_gen), color='red') + theme_bw() + labs(y='y')
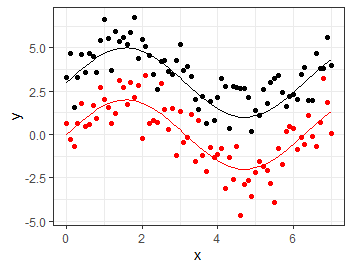
y_lm <- c(y_treat, y_ctrl) x_lm <- c(2*sin(x), 2*sin(x)) z_lm <- c( rep(1, x %>% length()), rep(0, x %>% length()) ) lm(y_lm ~ x_lm + z_lm) %>% summary() %>% tidy()
# A tibble: 3 x 5 # term estimate std.error statistic p.value # <chr> <dbl> <dbl> <dbl> <dbl> #1 (Intercept) -0.0660 0.119 -0.554 5.80e- 1 #2 x_lm 1.00 0.0621 16.1 1.22e-33 #3 z_lm 3.41 0.168 20.2 3.12e-43
問題なくできています.
2つの正弦関数の差は3にしてあったので, 大きく外れていませんね.
線形回帰で効果検証:さいごに
効果検証における回帰分析についてもっと詳しいことを知りたいときには下記の書籍をあたることをお勧めします.
この本を買う前に何となく内容を知りたいという方はこちらの記事が参考になるかと思います. またGoogleのdデータサイエンティストとして有名なTJOさんも効果検証入門を絶賛する記事をあげていらっしゃいます.
効果検証だけではなく, もっと線形回帰自体やその一般化について知りたい場合は次の書籍が参考になります. 一般化線形回帰や階層ベイズについても書かれています.