効果検証と合成コントロール
効果検証について勉強していた時に, 合成コントロールという方法に出会いました.
この方法はランダム化比較実験(= RCT, A/Bテスト)に比較してマーケティング実験におけるコストが低いという利点があります. その理由としてはコントロール群を用意せずとも, 介入対象ではないグループのデータから反実仮想データを作成して検証に用いることができるためです.
効果検証に関して日本における著名な書籍, 効果検証入門でも紹介されていて, 僕もこの本で知りました.
これらの手法では, 効果を検証したい施策の対象について施策が行われなかったときのデータが重要になります. しかし, 施策を対象の全体に行った場合は施策が行われなかったときのデータ, つまり「もしも~されなかったとしたらこうなっていた」という反実仮想データは得ることができません.
そこで, 合成コントロールが提案されました.
上記の効果検証入門では合成コントロールまで踏み込んで解説されていなかったので, 参考文献をたどって原著論文を調査してみました. 本記事は勉強した内容をまとめたものになります. 誤読している個所や勘違いしている個所に気づいた方はぜひコメントで指摘ください.
この記事は次の論文を読んで, その内容をRで実行してみたものになります.
Synth: An R Package for Synthetic Control Methods in Comparative Case Studies
効果検証と合成コントロール:合成コントロールって何?
すごく簡単にまとめると, 効果を検証したい対象のデータについてもしも介入がなかった場合のデータ(=反実仮想データ)を介入を受けていない他の対象のデータの加重平均で計算しようというものです.
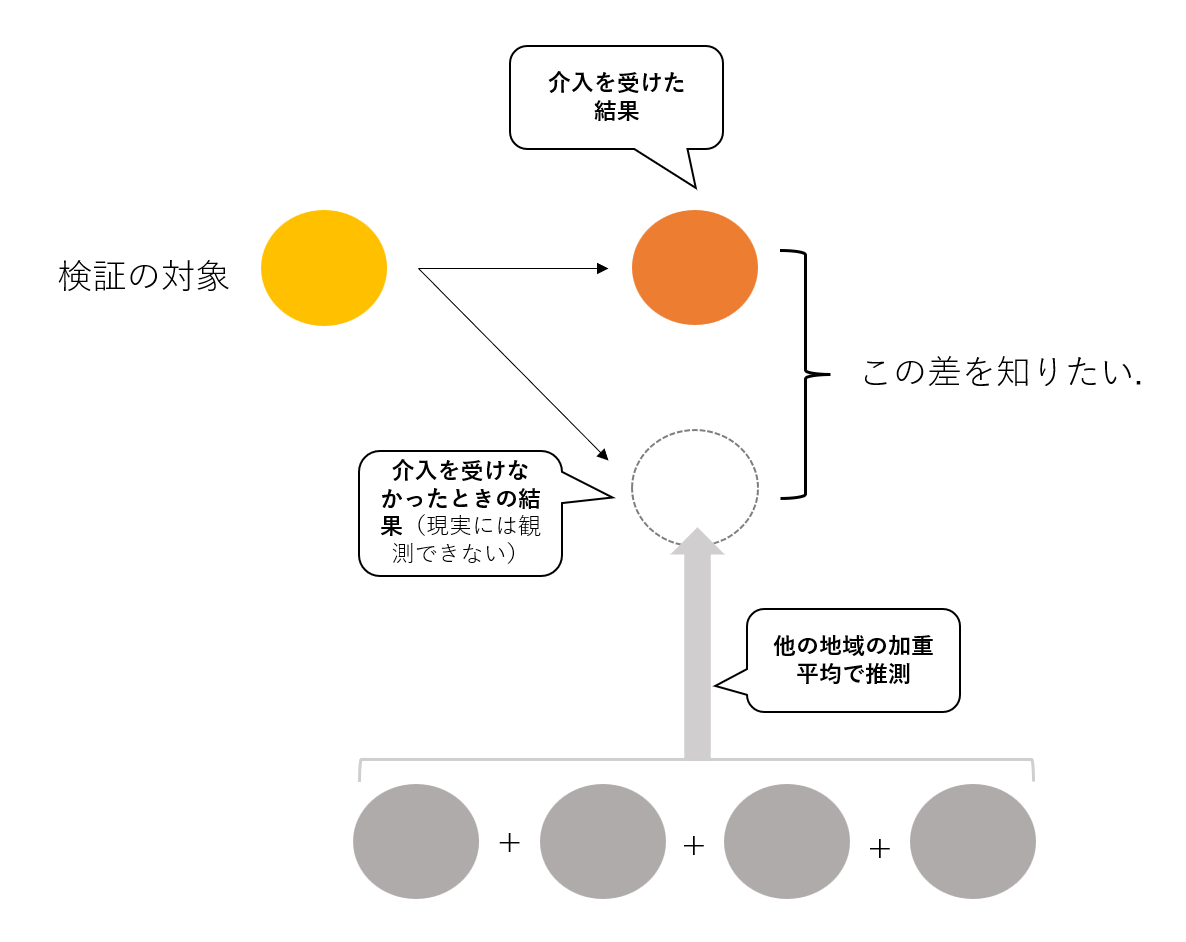
加重平均の重みを決定するためのプロセスを自動化してくれるのがSynthパッケージです.
後で再び出てきますが合成コントロールの結果として以下のような反実仮想データが得られます.
数理的な背景もきちんと書きたいと思っていたのですが, 次の記事を見つけてわかりやすかったのでリンクを貼るにとどめることにしました.
[R] CausalImpact でできること, できないこと(シンセティック統制法 (Synthetic Control Method))
合成コントロールで効果検証:データの観察
Synth: An R Package for Synthetic Control Methods in Comparative Case Studiesは合成コントロールを自動化してくれるRライブラリを紹介する論文です.
著者たちがソフトウェアの開発までやってくれています(すごい). 合成コントロールの数理的な仕組みもきちんとまとまっています.
では, まずは検証に用いるデータをよく観察してみます.
# 初回のみ
# install.packages("Synth")
library(Synth)
library(tidyverse) # Rといえばこれというくらい便利なtidyverse.
# データの読み込み
data(basque)
# データの情報
dim(basque)
## [1] 774 17
?basque
## 省略
basque[85:89, 1:4]
## regionno regionname year gdpcap
## 85 2 Andalucia 1996 5.995930
## 86 2 Andalucia 1997 6.300986
## 87 3 Aragon 1955 2.288775
## 88 3 Aragon 1956 2.445159
## 89 3 Aragon 1957 2.603399
データはフランス・スペインの国境にあるバスク地方の経済状況とそれに関連すると考えられるデータです.
この地域ではテロが発生し, その結果経済状況が悪化したと考えられていました. しかし, 経済状況の悪化が真にテロの影響であったのかを学術的に検証する調査は行われていませんでした.
そこで, abadie and gardeazabal 2003においてはじめて因果推論を用いた本格的な調査が実施されました. 上記のデータはこの論文で使用されたデータになります.
さて, 各地域の経済状況の指標として本データでは1人当たりGDPを採用しています. まずは, バスク地方と周辺地域の1人当たりGDPの推移を観察してみます.
# バスク地方を表す地域番号は17.
d_basque <- basque %>%
filter(regionno %in% c(2:18)) %>%
select(regionno, year, gdpcap) %>%
mutate(target = if_else(regionno == 17, "Basque", "Others")) %>%
mutate(regionno = paste("area", regionno, sep = "_"))
killing <- data.frame(
year = c(1968:1997),
death = c(2,1,0,0,1,6,19,16,17,11,67,76,92,30,37,32,32,37,41,52,19,19,25,46,26,14,13,15,5,13)
)
g <- ggplot() +
geom_line(d_basque, mapping = aes(x = year, y = gdpcap, group = regionno, color = target, size = target)) +
geom_bar(killing, mapping = aes(x = year,y = death/100 * 12), stat='identity', width=0.7, alpha = 0.2) +
geom_vline(xintercept = 1968, linetype = "dashed", alpha = 0.6) +
scale_y_continuous(
limits = c(0, 12),
sec.axis = sec_axis(~. /12 * 100, name = "テロによる死者数")
) +
theme_bw() +
theme(legend.position = "bottom") +
scale_colour_manual(values = c("black", "grey")) +
scale_size_manual(values = c(0.8, 0.5)) +
ggtitle("バスク地方と周辺地域の1人当たりGDP") +
ylab("1人当たりGDP(USD,1986)") +
xlab("Year")
plot(g)
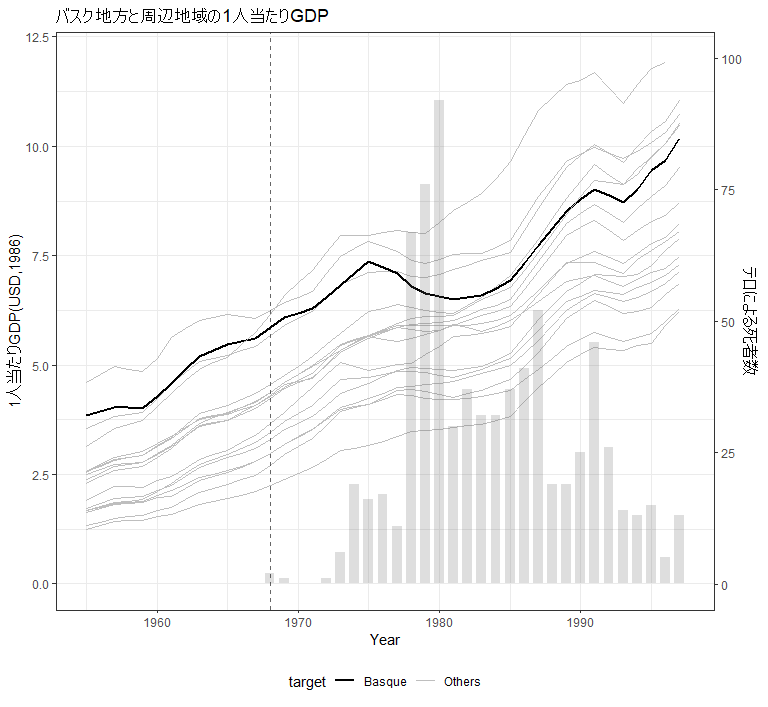
ETAと呼ばれるテロ組織が1968年から1990年代の半ばにかけて, バスク地方でテロ行為を行いました. その主な目的は資金調達で, ターゲットとなったのはバスク地方の起業家だったようです. その後, 起業家たちはバスク地方から逃げ出すことになります.
その結果, バスク地方の1人当たりGDPが低下したと考えられます.
上の図を見ると確かにテロによる死者数が増加するに従ってバスク地方の1人当たりGDPが下振れしている様子が見て取れます. 他にも下振れしている地域があるようですが, バスク地方の下振れは他の地域よりも大きな変化であるように見えます.
これを実証してみましょう.
合成コントロールで効果検証:反実仮想データの作成
効果検証のためにはテロという介入がなかった場合に, バスク地方の1人当たりGDPがどのように推移したかを予測する必要があります.
合成コントロールを用いると反実仮想データを, 介入がなかった他の地域の加重平均を算出することで作成します. そして, その加重平均の重みまで自動的に計算できるよう数理的に設計されているのが合成コントロールです.
最終的にデータから作成される二次形式を最小化する問題に帰着されます(二次形式を定義する行列も自動で選んでくれるようです).
実行自体はたったの2ステップです.
1. dataprep()の実行
合成コントロールを実行するメインの関数synth()を実行する前に, データの前処理を自動で行ってくれるdataprep()を実行します.
dataprep()は元データと各種オプションを渡すと,\(X_1, X_0, Z_1, Z_0\)という4種類のベクトルを返します. 各ベクトルが何を意味するのかの詳しい説明は原著論文を読んでもらいたいと思います.
\(Z_1, Z_0\)は二次形式を決める行列\(V\)の計算に使用される制約条件の時系列です. dataprep()のなかで調整できます.
dataprep()を実行します.
dataprep.out <- dataprep(
foo = basque,
predictors = c( # 共変量の指定
"school.illit",
"school.prim",
"school.med",
"school.high",
"school.post.high",
"invest"
),
predictors.op = "mean",
time.predictors.prior = 1964:1969, # 介入前期間の指定
special.predictors = list( # Z_iの調整
list("gdpcap", 1960:1969, "mean"),
list("sec.agriculture", seq(1961, 1969, 2), "mean"),
list("sec.energy", seq(1961, 1969, 2), "mean"),
list("sec.industry", seq(1961, 1969, 2), "mean"),
list("sec.construction", seq(1961, 1969, 2), "mean"),
list("sec.services.venta", seq(1961, 1969, 2), "mean"),
list("sec.services.nonventa", seq(1961, 1969, 2), "mean"),
list("popdens", 1969, "mean")),
dependent = "gdpcap", # 目的変数の指定
unit.variable = "regionno", # 各地域を識別する変数の指定
unit.names.variable = "regionname",
time.variable = "year", # 時刻を表す変数の指定
treatment.identifier = 17, # 介入群の指定
controls.identifier = c(2:16, 18), # コントロール群の指定
time.optimize.ssr = 1960:1969, # 最適化する期間の指定
time.plot = 1955:1997 # グラフ化する際に使用する期間の指定
)
出力を確かめると以下のようになります.
dataprep.out$X1 # 17 # school.illit 39.888465 # school.prim 1031.742299 # school.med 90.358668 # school.high 25.727525 # school.post.high 13.479720 # invest 24.647383 # special.gdpcap.1960.1969 5.285468 # special.sec.agriculture.1961.1969 6.844000 # special.sec.energy.1961.1969 4.106000 # special.sec.industry.1961.1969 45.082000 # special.sec.construction.1961.1969 6.150000 # special.sec.services.venta.1961.1969 33.754000 # special.sec.services.nonventa.1961.1969 4.072000 # special.popdens.1969 246.889999 dataprep.out$Z1 # 17 # 1960 4.285918 # 1961 4.574336 # 1962 4.898957 # 1963 5.197015 # 1964 5.338903 # 1965 5.465153 # 1966 5.545916 # 1967 5.614896 # 1968 5.852185 # 1969 6.081405
2. synth()の実行
こちらがメインの関数になります.
実行することはdataprep()の結果をsynth()に渡すだけです. つまり, 重要な調整はすべて前処理用の関数dataprep()のオプション指定ですべて終了していいてあとは結果を計算するだけということです.
# 合成コントロールの実行
synth.out <- synth(data.prep.obj = dataprep.out, method = "BFGS")
# X1, X0, Z1, Z0 all come directly from dataprep object.
#
#
# ****************
# searching for synthetic control unit
#
#
# ****************
# ****************
# ****************
#
# MSPE (LOSS V): 0.008864606
#
# solution.v:
# 0.02773094 1.194e-07 1.60609e-05 0.0007163836 1.486e-07 0.002423908 0.0587055 0.2651997 0.02851006 0.291276 0.007994382 0.004053188 0.009398579 0.303975
#
# solution.w:
# 2.53e-08 4.63e-08 6.44e-08 2.81e-08 3.37e-08 4.844e-07 4.2e-08 4.69e-08 0.8508145 9.75e-08 3.2e-08 5.54e-08 0.1491843 4.86e-08 9.89e-08 1.162e-07
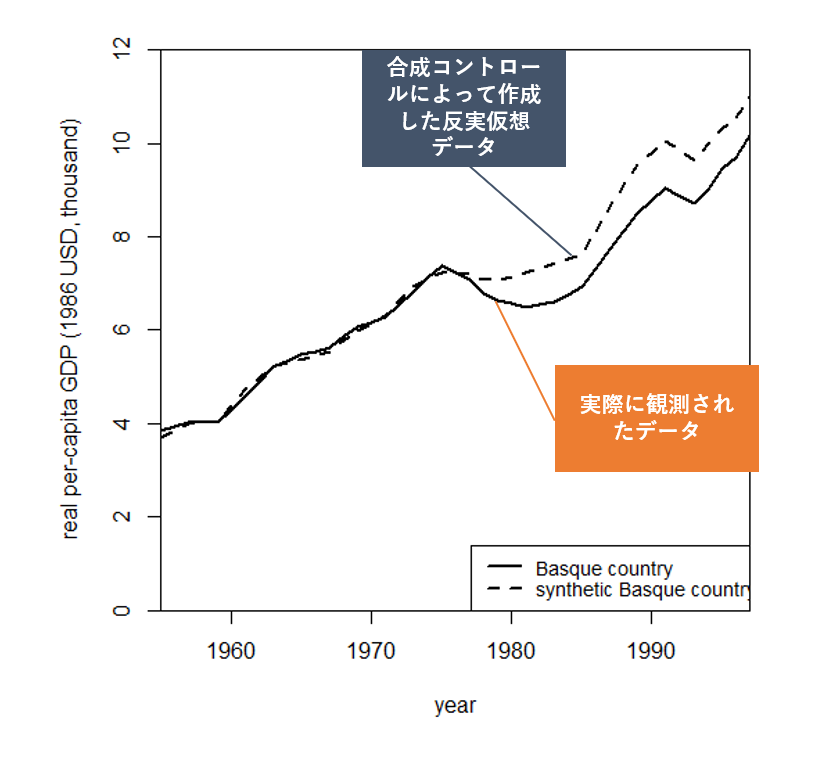
path.plot(
synth.res = synth.out,
dataprep.res = dataprep.out,
Ylab = "real per-capita GDP (1986 USD, thousand)",
Xlab = "year",
Ylim = c(0, 12),
Legend = c("Basque country", "synthetic Basque country"),
Legend.position = "bottomright"
)
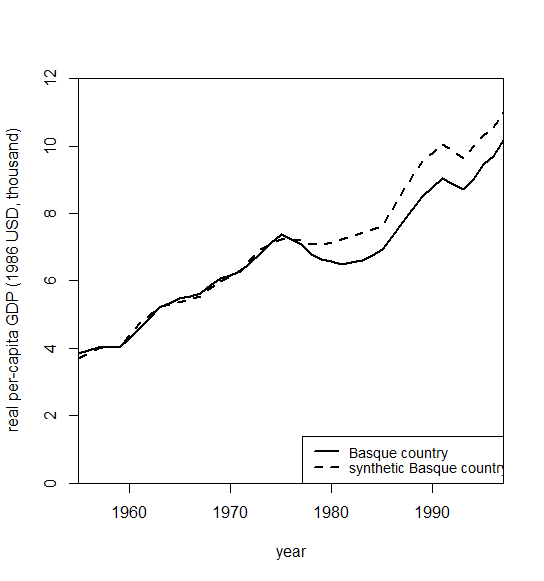
図を見ると, 介入が始まる前(=テロ行為が始まる前)におけるコントロール群の当てはまりが非常によく, 介入開始後の期間の「もしも介入がなかった場合」のデータである反実仮想データになってることが見て取れます.
合成コントロールで効果検証:プラセボテスト
続いて, 上記のプロットからテロの効果で1人当たりGDPが低下したと結論付けてよいのか検討します.
その方法としてプラセボテストという手法が推奨されています. この手法はバスク地方のデータに対して行った計算と同様の計算をほかの地域のデータに適用して, その結果1人当たりGDPの低下バスク地方ほど起きないことを確認する手法となります.
まず, バスク地方の反実仮想データと観測データの差をプロットしてみます.
# 差の出力 gaps.plot( synth.res = synth.out, dataprep.res = dataprep.out, Ylab = "gap in real per-capita GDP (1986 USD, thousand)", Xlab = "year", Ylim = c(-1.5, 1.5), Main = NA )
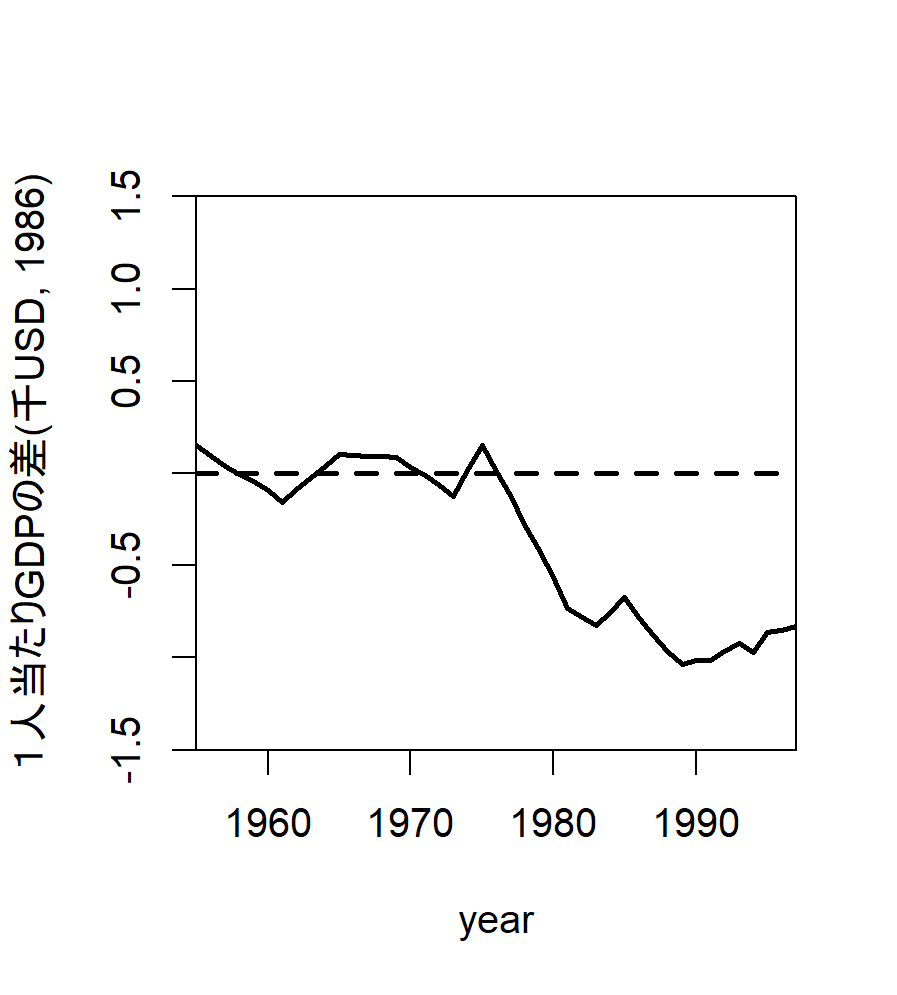
続いて上で実行した合成コントロールと全く同じ計算を対象地域だけを変えながら繰り返し行います. そして, 得られた反実仮想データと観測データの差を同じようにプロットしていきます.
少しコードが長いのでデフォルトでは非表示にしてあります.
# codes
この結果をプロットしていくと以下のようになります.
mspe_of_Basque <- results %>%
filter(regionno == 17) %>%
pull(mspe) %>%
unique()
results_low_mspe <- results %>%
filter(mspe < 5 * mspe_of_Basque) %>%
mutate(regionno = paste("area", regionno, sep = "_") %>% as.factor()) %>%
mutate(area = if_else(is_Basque == "1", "Basque", "Others"))
results_low_mspe$regionno %>% fct_inorder() %>% fct_shift(., n = -1)
killing <- data.frame(
year = c(1968:1997),
death = c(2,1,0,0,1,6,19,16,17,11,67,76,92,30,37,32,32,37,41,52,19,19,25,46,26,14,13,15,5,13)
)
ggplot() +
geom_line(results_low_mspe, mapping = aes(x = year, y = gaps, group = regionno, color = area, size = area)) +
geom_bar(killing, mapping = aes(x = year,y = death/100), stat='identity', width=0.7, alpha = 0.3) +
geom_vline(xintercept = 1968, linetype = "dashed", alpha = 0.6) +
scale_y_continuous(
limits = c(-2,1.5),
sec.axis = sec_axis(~.*100, name = "テロによる死者数")
) +
theme_bw() +
theme(legend.position = "bottom") +
scale_colour_manual(values = c("black", "grey")) +
scale_size_manual(values = c(0.8, 0.3))
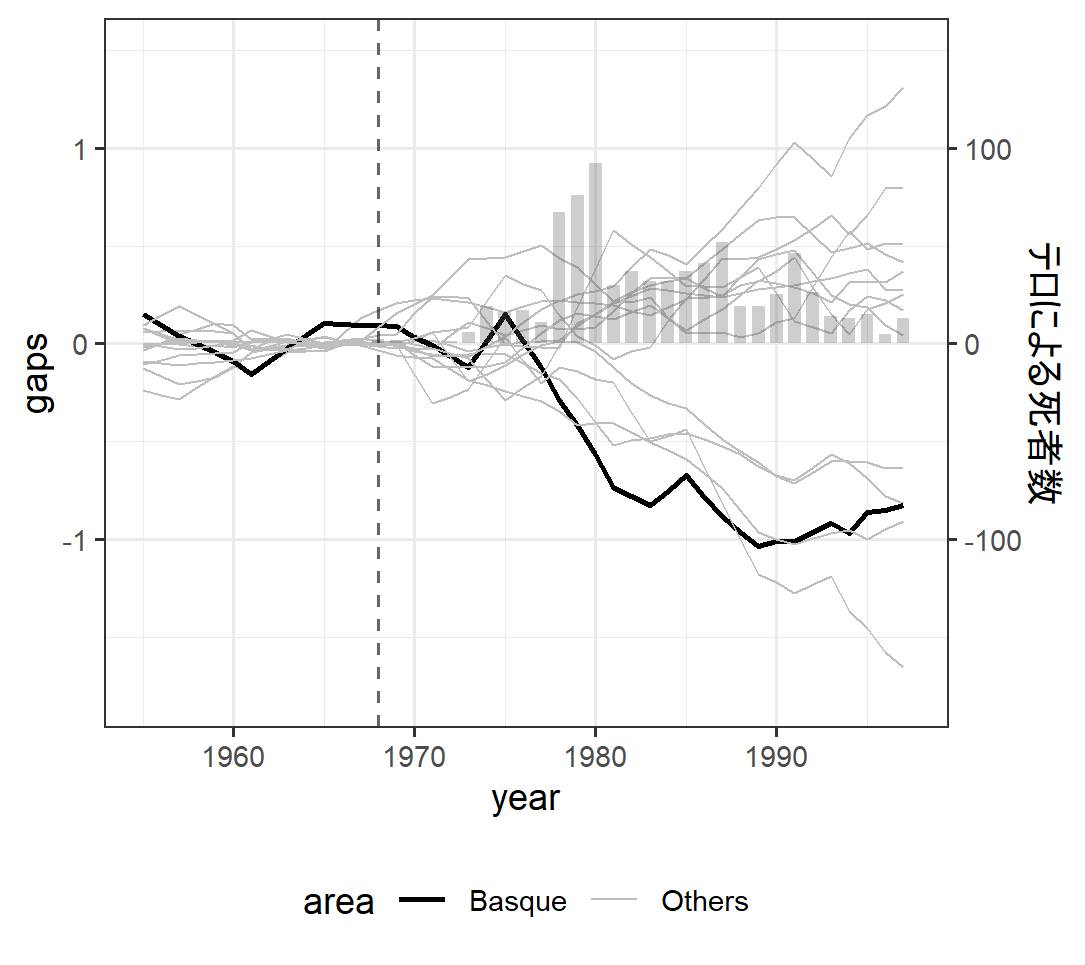
論文では上記の図をもって「テロの影響を他の地域に再当てはめしてもバスク地方ほどの差を得る確率は非常に低い」としています.
ここに関してどのように判断しているのかまだ少し理解しきれていません. 他の地域でもテロ開始後に数値が下がっているところがないわけではありません. 一方, テロによる死者数の増加に伴って(特に1980年前後に)最も急な大きな減少を見せているのはバスクであることは事実であるようです.
因果推論においてこの最終的な判断の部分も難しい点の1つだと思うので他の論文や書籍を参考にしながら知識と勘を身につけていければと思います.
合成コントロールで効果検証:まとめ
論文を参考にSynthパッケージを使用してみました.
印象としては,
dataprep()のオプションの調整が自分でやってみると思ったより難しい・p値や確信区間のように数字で効果の有無をはっきり言えるわけではない点が気になる(こいつらもはっきり言えてるかは議論があるかと思いますが少なくとも数値に落とし込める)
という点が気になりました. すぐに実務に生かせそうかは今のところなんとも言えません. 効果検証・因果推論のテーマは他にもたくさん勉強すべきことがありそうですので, この他にもBSTSやCausalImpactなどいろいろ触ってまずは視野を広げていきたいと思います.
参考文献
[1] Abadie, Alberto, Alexis Diamond and Jens Hainmueller. “Synth: An R Package for Synthetic Control Methods in Comparative Case
Studies.” Journal of Statistical Software, June 2011, Volume 42, Issue 13, p.1-17.
[2] Abadie, Alberto, Alexis Diamond and Jens Hainmueller. “SYNTHETIC CONTROL METHODS FOR COMPARATIVE CASE STUDIES: ESTIMATING THE EFFECT OF CALIFORNIA’S TOBACCO CONTROL PROGRAM” NBER Technical Working Paper No. 335 January 2007, Revised July 2007.
[3] Alberto Abadie and Javier Gardeazabal. “The Economic Costs of Conflict: A Case Study of the Basque Country” The American Economic Review, Vol. 93, No. 1 (Mar., 2003), pp. 113-132.
[4] 安井翔太, 効果検証入門 -正しい比較のための因果推論/計量経済学の基礎-, 技術評論社2020.