この記事の内容
今回はこの範囲です.
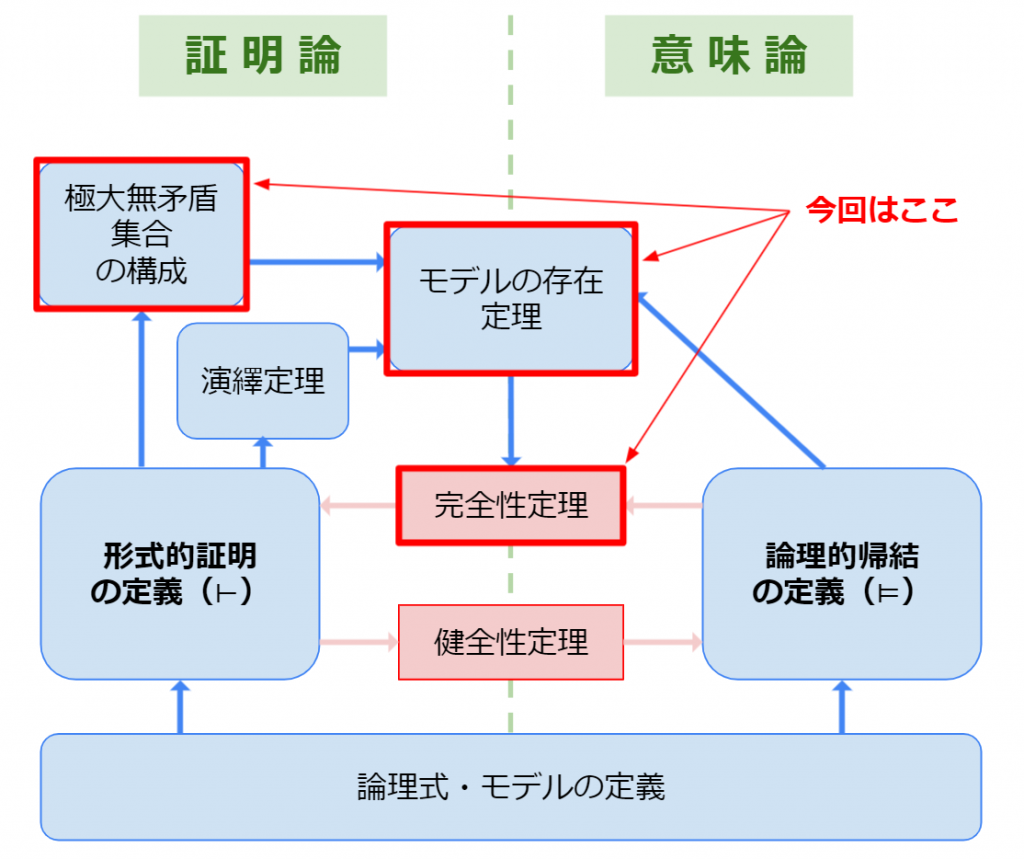
モデルの存在定理
ここまでの準備があればあとは完全性定理までもう少しです.
実際,モデルの存在定理を示せれば完全性は系として簡単に導けます.では早速,モデルの存在定理を示しましょう.
前回少し述べましたが,モデルの存在定理を示す際に極大無矛盾集合を構成します.
定義(矛盾・無矛盾):
論理式の集合\( \Gamma \)が\( \bot \)を導くとき,つまり\( \Gamma \vdash \bot \)となるとき,\( \Gamma \)は矛盾するという.\( \Gamma \)が矛盾しないとき\( \Gamma \)は無矛盾であるという.
定理(モデルの存在定理):
論理式の集合\( \Gamma \)が無矛盾であるとき, \( \nu \vDash \Gamma \)なる付値\( \nu \)が存在する.
(証明)
(1)極大無矛盾集合の構成.
素論理式の集合\( I \)は可算であったからそこから作られる論理式全体の集合も可算となる(*)ため,論理式全体を\( A_0, A_1, A_2, \cdots, \)と一列に並べる.このとき,論理式の集合の増加列\( \{ T_n \} \)を次で定める.
\( \quad T_0 := \Gamma, \)
\(
\quad
T_{n+1} :=
\begin{cases}
T_{n} \cup \{ A_n \}, \quad (T_{n} \cup \{ A_n \}\text{が無矛盾のとき}) \\\
\\\
T_{n} \cup \{ \lnot A_n \}. \quad (T_{n} \cup \{ A_n \}\text{が矛盾するとき})
\end{cases}
\)
定義より各\(n\)について\(T_n\)は無矛盾であり,したがって\( T = \bigcup_n T_n \)も無矛盾である.実際,\(T\)が矛盾したと仮定すると,証明の定義から\(S \subset T\)なる有限部分集合\(S\)が存在して\( S \vdash \bot \)となる.このとき,ある\(n\)について\(S \subset T_n\)となるが,これは\( T_n \vdash \bot\)を意味し,\(T_n\)の無矛盾性に矛盾する.
また,構成法より\(T\)は次の性質を満たす.
\( \quad \text{任意の論理式} \varphi \text{について}, \varphi \in T \text{または} \lnot \varphi \in T.\)
この性質を極大性という.
(2)モデルの構成.
付値\( \nu \)を,
\(
\quad
\nu(A) :=
\begin{cases}
1, \quad (A \in T\text{のとき}) \\\
\\\
0, \quad (\lnot A \in T\text{のとき})
\end{cases}
\)
で定める.
このとき,任意の論理式\( \varphi \)について\( \nu (\varphi) = 1 \iff \varphi \in T \)が成り立つ.これは\(T\)の極大性と無矛盾性,演繹定理を用いることによって示される.
ここで\(\Gamma \subset T\)であるから\(\nu\)は\(\Gamma\)のモデルである.
最後の部分は少し省略しています.各論理記号について,
\( \quad \varphi, \psi \in T \iff \varphi \land \psi \in T ,\)
\( \quad \varphi \in T \text{または} \psi \in T \iff \varphi \lor \psi \in T ,\)
\( \quad \lnot \varphi \in T \text{または} \psi \in T \iff \varphi \rightarrow \psi \in T ,\)
を示せばよいわけですが,これはそれぞれ手を動かして確かめるのが一番良いと思います.やってみるとすべて書き出すほどの難易度ではないわりに文の量が多くなってしまいます.
完全性定理
いよいよ完全性定理に到達しました.もうここまでくればあまり難しくありません.
定理(完全性定理):
\( \Gamma \vDash \varphi \Rightarrow \Gamma \vdash \varphi \)
(証明)
\( \Gamma \not\vdash \varphi \)とする.このとき,演繹定理より,\( \Gamma \cup \{ \lnot \varphi\}\not\vdash \bot \)となる.よって,モデルの存在定理より\( \nu \vDash \Gamma \cup \{ \lnot \varphi\} \)なる付値\( \nu\)が存在する.この\( \nu \)は\( \nu \not\vDash \varphi\)を満たす.したがって,\( \Gamma \not\vDash \varphi. \)
これで完全性定理を示すことができました.
参考文献
[1] 新井敏康,数学基礎論 増補版,東京大学出版会,2021.
[2] ケネス・キューネン, キューネン数学基礎論講義, 日本評論社,2016.
[3] 鹿島亮, 現代基礎数学15 数理論理学, 朝倉書店, 2009.