本連載の特徴
命題論理に焦点を絞ることで完全性定理までをコンパクトに、かつ厳密さを保ったままわかりやすく解説するのが本連載の目的です。
命題論理は数理論理学を学ぶ上ではとても基本的で重要な部分です。Henkinの方法を用いれば命題論理の結果(つまり健全性や完全性)を一階述語論理にまで拡張することができます。また、数理論理学的な考え方に慣れるという意味でも命題論理に慣れることは重要です。
そこで、この連載では命題論理の定義から完全性までをコンパクトにわかりやすく整理していきます。
命題論理の全体観
ここで連載を通して展開する議論の概観を抑えたいと思います.細かい議論に入る前の地図のような役割です.
いまからやっていくことは次の図に集約されます.
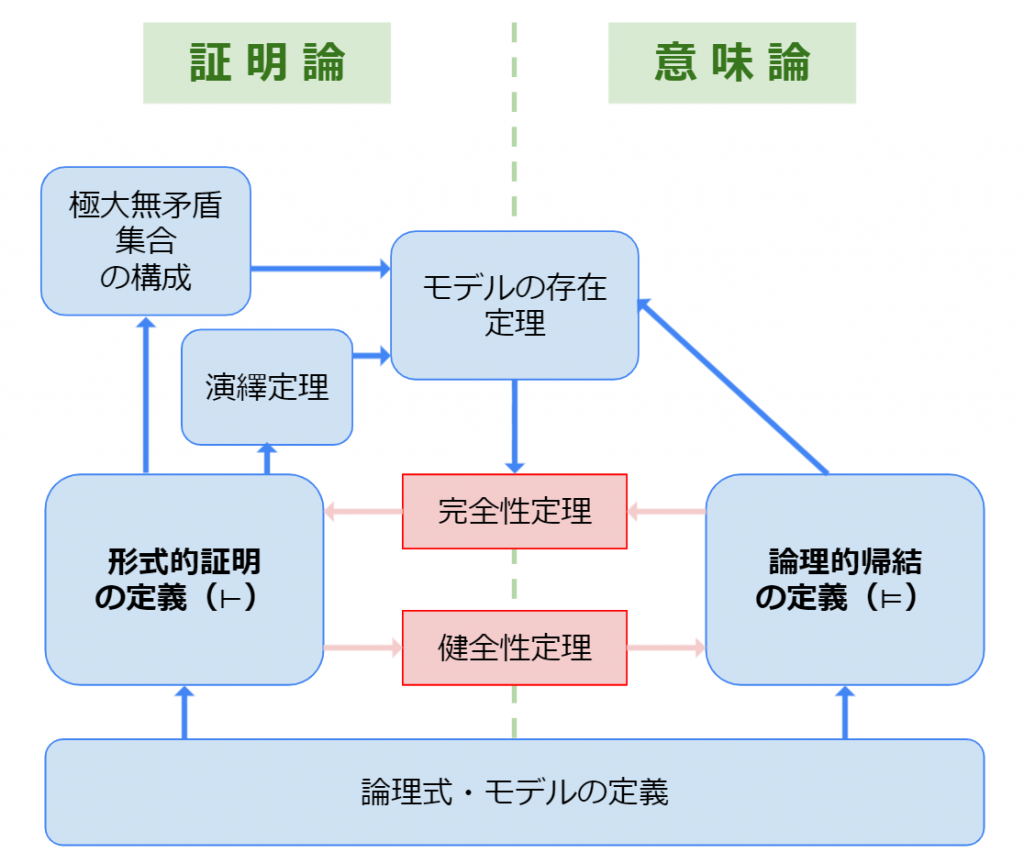
この図はあくまで全体をわかりやすく俯瞰するためのものなので必ずしも唯一正しい図であるとは言いません.たとえば,モデルの定義は意味論に入ると考えても特に問題はないですし,証明論を構文論と呼ぶ場合もあります.このあたりは好みでよいと思います.
大切なのは各定理をきちんと証明できて,健全性と完全性が示せることです.
また,少し細かい話をすればこの地図通りに議論を展開する必要はありません.数理論理学の教科書はたくさんありますが,どの教科書を図にしても微妙に異なる図になるはずです.上の図はいくつかの教科書を参考に筆者がもっとも頭に入りやすいと感じた地図です.
参考にした書籍は主に新井本[1],キューネン本[2],鹿島本[3]です.どの本も国内で数理論理学を学ぶ人々にとっては標準的でしょうし,新井本に至っては王道に近い印象を持っています.
命題論理の特徴
命題論理の特徴は、命題変数というものを導入して「命題の中身には立ち入らない」という立場をとります。つまり、\(A\)という命題があったときにその命題の意味は考えず、\(A\)が真か偽かのみを問題にします。
大雑把に言えば高校1年性でやる論理の性質をもっと厳密に研究したものが命題論理だと行って仕舞えばわかりやすいかもしれません。
目指すところ
数理論理学の1つの目的は数学における証明を研究の対象にすることだと言えます。
数学をするときには様々な命題、定理を証明します。しかし通常、証明するとはどういうことか、論理的に正しいとはどういうことかをきちんと定義するということはありません。数学のどの分野でも証明という営みを習って実際にやってみて身体で証明とは何かを理解します。
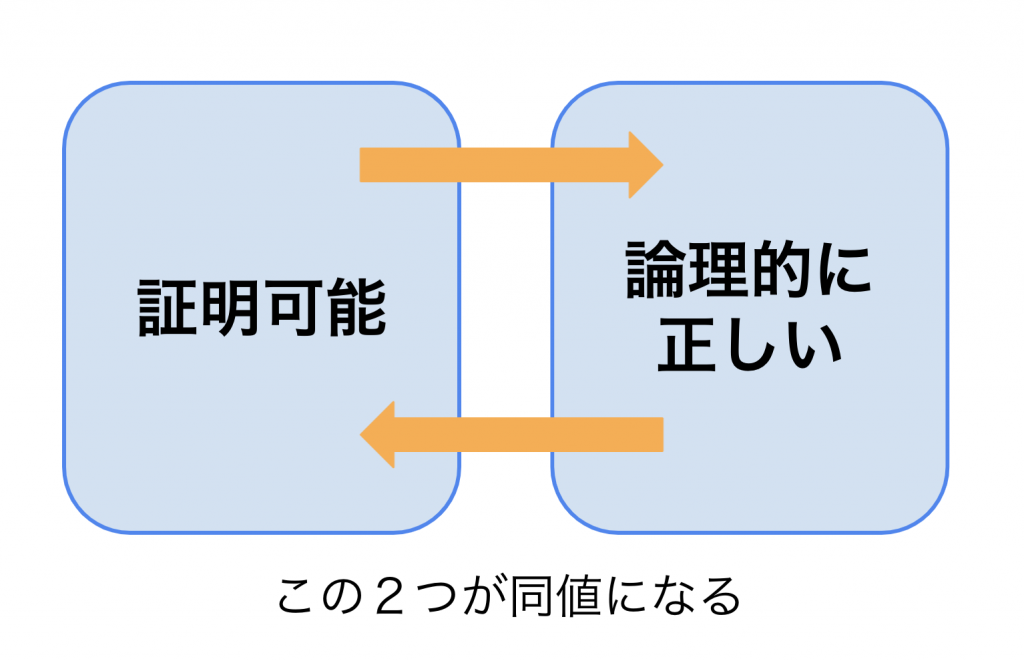
数理論理学ではその部分を曖昧にせず、「証明可能とは何か」「論理的に正しいとは何か」をきちんと定義して、「証明可能であれば論理的に正しいし、論理的に正ければ証明可能である」ということを数学的に証明していきます。
実はこの「証明可能であれば論理的に正しいし、論理的に正ければ証明可能である」という主張こそが命題論理の健全性と完全性です。
参考文献
[1] 新井敏康,数学基礎論 増補版,東京大学出版会,2021.
[2] ケネス・キューネン, キューネン数学基礎論講義, 日本評論社,2016.
[3] 鹿島亮, 現代基礎数学15 数理論理学, 朝倉書店, 2009.